Intressanta matematiska fakta för dem i världen vill veta mer om

Layfhaker undrade hur viktigt matte är i vårt dagliga liv. Är det överhuvudtaget någon annan behövs? Svaret på denna fråga har hittat i boken Nelly Litvak och Andrew Raigorodskii "Vem behöver matte? Förståeligt bok om hur den digitala världen. "

Vad denna bok?

Om matematik. :) Mer specifikt av de delar av det som är mest efterfrågade inom logistik, transport scheman, kryptering och kodning av data. Författare på de tillgängliga exemplen visar hur matematiken hjälper till att spara tid och pengar, spara dina data under tillförlitligt skydd och för att välja en kö i butiken.

Vad är linjär programmering

I det här fallet talar vi inte om programmering i sig. Det är snarare en process av optimering. Varför är linjär? Eftersom vi talar bara om linjära ekvationer: när variablerna att addera, subtrahera eller multiplicera numret. Inga exponentiations eller multiplikationer. Sådan programmering hjälper till att minimera kostnaderna för varor eller tjänster (om vi talar om handel) eller öka intäkterna.

Linjär programmering används inom oljeindustrin, liksom inom logistik, planering, schemaläggning.

Kort sagt, som ett exempel, ser det ut som.

Föreställ dig att du är engagerad i försäljningen av plåtar. En kund har beställt dig till 70 ark, och den andra - 30 ark. I detta fall är dina reserver lagras i olika lager, som vart och ett har mindre än 100 ark. Din uppgift - att minimera kostnaderna för transport av tenn kunder.

Här kommer in den linjära ekvationen. Vi kommer inte att prata i detalj hur detta problem löses i boken, men efter några steg av beräkningarna är det bästa alternativet, som låter dig spara 12% av kostnaden för leverans jämfört med de kostnader som skulle behöva lida om du inte använder den matematiska närma.

Nu föreställa sig att det inte handlar om leverans av flera ark av tenn och på schemat och tunga järnvägstrafiken i hela landet. Och sedan 12% - detta är antalet flera nollor i slutet.

Varför den bästa lösningen är inte alltid det mest bekväma?

Matematik - vetenskapen om exakta och vackra. Men inte alltid lösningen av problemen verkar ganska lämpligt. Det hände med schemat för järnvägstransporter i Nederländerna. I denna lilla land tåg och tåg är mycket populära. Transport schemat är så föråldrad som håller på att hända var en riktig kollaps.

Därför beslutades att utarbeta ett nytt schema 2002. Experterna hade perfekt tänka på antalet bilar, de stannar, ankomst- och avgångstider, för att inte tala om schemat för lokförare och konduktörer till 5500 tåg per dag.

Som ett resultat av den ideala ur en matematisk synvinkel var schemat upprättats. Och som alla borde vara lyckliga. Men inte passagerare: stop för kort, för vagnar lastade, ingen tröst. Det hände på grund av matematik lösa matematiska problem bara. Och vem är att skylla det faktum att ledningen är lame?

Är det möjligt att koda något?

Vanliga datoranvändare är svårt att föreställa sig att alla bilder, videor, texter, sånger - Detta är inte bilder, videor, texter och låtar som ettor och nollor, ettor och nollor.

Att koda texten lättare att: för varje bokstav, siffra eller skiljetecken för att komma fram till en sekvens av ettor och nollor. Men hur är det med färg? Lyckligtvis upptäckte fysiker att varje färg - en kombination av rött, blått och grönt. Och det innebär, och färgerna kan omvandlas till tal.

Varje färg har 255 nyanser. Till exempel orange - rött 255 och 128 grön, blå - 191 grön och 255 blå. Och om färgen kan uttryckas i siffror, betyder det att det kan placeras i en dator, TV eller mobiltelefon.

Med video ännu svårare - för mycket information. Men matematiker hittat en väg ut ur denna situation och har lärt sig att komprimera data. Den första rutan av filmen kodas helt, och sedan kodas bara ändrar.

Problem var bara med musiken. Forskarna har fortfarande inte lärt sig hur man koda musik så att det lät så klart, som i livet. Eftersom musiken inte kan utökas till "nyanser", som kan skrivas i den digitala domänen.

Varför internet aldrig raster?

Nej, detta är inte ett verk av dina leverantörer, som ibland kunde vara bättre. Det handlar om varför, till exempel Google svarar alltid på våra förfrågningar, är anledningen till att vi kan alltid tillgång till rätt platser, och varför interferens (och det finns faktiskt en hel del) inte avskurna vår tillgång till World Wide Web.

Det korta svaret på denna fråga är, i mitten av förra århundradet, två matematiker Paul Erdos och Alfred Renyi öppnade världens slump grafer. Counts - denna bild av noder sammankopplade med linjer. Nu, tänk dig att enheterna - en dator, och linjerna - kommunikationslinjer. Om du tar räkna till 100 datorer, kommer det att se ut så här:

Och Renyi och Erdash genom att utmana för humaniora och dator enkelt för tekniker kom till en fantastisk avslutning. Ju fler datorer i nätverket, desto mer länkarna mellan dem, desto mindre sannolikt att orsaka störningar, det vill säga en som kommer att lossna oss från en värld av obegränsad kommunikation och ändlösa information.

Om du inte tror mig, här är ett bord.

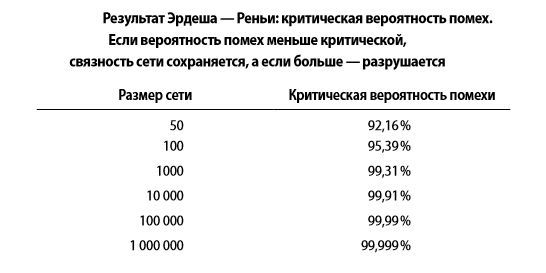
Det vill säga, om någon kanal bryts, nästan alltid möjligt att gå på en annan kanal och få kontakt med spegeln i fråga.

Vad är den plats på Internet och hur man undviker den?

Visste du att varje gång genom att fråga Google eller gå till en webbplats, du befinner dig på en plats? Naturligtvis går det mycket snabbare än du kommer till kassan i snabbköpet, och du nästan inte märker avbrottet, men ändå om någon har begått alltför global fråga kräver mer tid på det bearbetning.

Så du måste välja servern där all det minsta, eller en i kön som ingen tung fråga.

Och här träder i kraft vanligtvis ett val av två. Informatik Derek Eager, Edward och John Lazovsky Zahordzhan 1986 och erbjöd sig att bevisa teorin att om begränsa utbudet av servrar, som kommer att skickas till din begäran upp till två, då är sannolikheten för slip tur ökar ibland.

Låt oss titta på exemplet med snabbköpet. Innan du en hel del fonder med olika ledningslängd. Du har alternativ: slumpmässigt välja den första tillgängliga eller stopp vid två och välj den där alla mindre. Så du slutför köpet snabbare med en högre sannolikhet.

Teorin om de fyra handskakningar

Många har hört att alla människor i världen är bekanta med varandra efter sex handslag. Denna teori fortfarande på 1960-talet visade sociologen Stanley Milgram, frågar människor från olika stater att skicka ett brev till en person. Brevet var tvungen att först skicka sin vän, som i sin tur skickade henne - och så länge som brevet aldrig nått adressaten. Som ett resultat, var kedjan bara sex.

Det var inte förrän så länge som Facebook anställda inte riktar sig till forskare återigen för att bekräfta eller vederlägga denna teori. Efter bearbetning alla möjliga par bekanta bland alla användare i nätverket, visade det sig att denna kedja är ännu kortare. Och det är bara 4,7! Kan ni föreställa er? Mellan varje människa på jorden, och du bara 4,7 handskakning!

Ska jag läsa den här boken?

Ja, om du också vill veta hur datakryptering, som bröt koden "Enigma", som är reklam auktioner på Google och "Yandex", liksom djupare in i en värld av matematiska problem och ekvationer.

Layfhaker sagt inte alla intressanta fakta underhållande matematik, så om du vill komplettera sina kunskaper inom detta område kommer boken "Vem behöver math" säkert bevisa för dig användbara.

Trots enkelheten i presentationen, om du är en humanitär, medan läsning, kan du behöva en matematisk handbok.

Köp tryckt bokKöp e-bok